Month: June 2021

A recursive function may be unfamiliar, especially to a beginner. This is because the concept is abstract, so that we don’t realize the opportunity to use it.

In this post, a brief description and an example of a recursive function are introduced. Through this example, the readers may realize it is helpful to keep your code simple.

What is a Recursive function?

A recursive function is a function that calls itself.

For example, the following code is the simple example.

It should be noted that, as a sensible reader may notice, running this function leads to an infinite loop.

def func():
  print("This is a recursive function!")
  """Call itself!!"""
  func()

print(func())

When to use it?

A function is a converter that performs one process. Therefore, a recursive function would be practical when creating a function that does the same thing multiple times.

Replacing similar processing with a recursive function leads to code simplification. Let’s experience it with the following simple example.

Example: factorial calculation

Here, one example is introduced. We will create the function for factorial calculations. Factorial calculations are like below.

$$N!=N\times(N-1)\times…\times2\times1$$

Without Recursive function

First, let’s implement without a recursive function. The code is below.

"""factorial calculation without recursive function"""
def factorial_nonrecursive(x):
  result = 1
  """N!=1*2*...*(N-1)*N"""
  for i in range(1, x+1):
    result = i*result
  return result


"""ex. 4! = 1*2*3*4 = 24"""
result = factorial_nonrecursive(4)
print(f"factorial: {result}")


>> factorial: 24

It may seem complicated at first glance, but the above code is just multiplying in order from 1 using for loop.

With Recursive function

Next, we perform refactoring of the above code with a recursive function. The code after refactoring is as follows.

"""factorial calculation with recursive function"""
def factorial_recursive(x):
  if x == 1:
    return 1
  else:
    return x*factorial_recursive(x-1)


"""ex. 4! = 1*2*3*4 = 24"""
result = factorial_recursive(4)
print(f"factorial: {result}")


>> factorial: 24

Did you realize that the code has become so simple?

Since the code is simple, it is easy to understand that the “factorial_recursive(x)” performs multiplication of the argument “x” with the previous returned result of this function.

Appendix: about Computational Cost

Here, we check the computational cost. We compare the calculating times between the above functions we created.

We import the necessary modules.

from time import time  # calculate time
import sys
sys.setrecursionlimit(50000) # Set the upper limit of the number of recursion
import numpy as np
from matplotlib import pyplot as plt

By the following codes, we get the time from begin to finish of calculating $N!$, where $N=10000$.

The first is the case with a recursive function.

N = 10000
cal_time_recursive = []
for i in range(1, N+1):
  begin_time = time()
  result = factorial_recursive(i)
  end_time = time()
  cal_time_recursive.append(end_time - begin_time)

The second is the case without a recursive function.

N = 10000
cal_time_nonrecursive = [] # calculation time
for i in range(1, N+1):
  begin_time = time()
  result = factorial_nonrecursive(i)
  end_time = time()
  cal_time_nonrecursive.append(end_time - begin_time)

Finally, let’s check the graph of the calculation time of N! For N. The red and blue lines indicate the with-recursive and without-recursive cases, respectively.

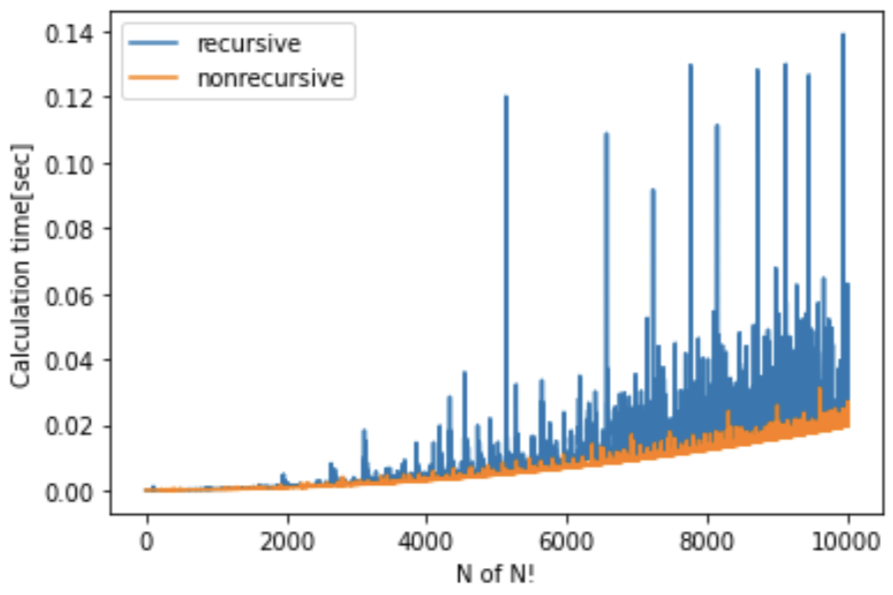
You can see that the calculation time tends to be longer overall with recursion. This result would be due to the increase in the number of processes associated with the function calling itself sequentially. As you can see, recursive functions can simplify your code, but in some cases, they can take longer than usual.

Summary

A recursive function is a function that calls itself. Although it is unfamiliar with a python beginner, it is helpful to keep your code simple.

If you come across a situation where you can use it, please use it positively.