Step-by-step to a Data Scientist

October 24, 2020December 24, 2020

Python Shortcode for Linear Regression

Step-by-step to a Data Scientist > Blog > Machine Learning

Linear regression analysis is one of the most basic data analyses. This method is based on the relationship between independent variables and dataset. Therefore, if the fit between the linear model and the dataset is well, an analysis with high model interpretability can be performed.

Purpose of this post

The purpose is to introduce the shortcode example for linear regression.

Explanation of Linear Regression

In this post, we just check the brief concept of linear regression. The details are introduced in another post. Please refer to it.

Brief Explanation of the Theory of Linear Regression

A representation of a linear regression is as follows:

$$y =\omega_{0}+\omega_{1}x_{1}+\omega_{2}x_{2}+…+\omega_{N}x_{N},$$

where $x_{i}$ is an independent variable and $\omega_{i}$ is a coefficient.

Here, for convenience, we adopt just one independent variable model. This is the most simple form everyone knows.

$$y =\omega_{0}+\omega_{1}x_{1}.$$

Training Dataset

We create the training dataset from the following code. How to create is introduced in another post.

import numpy as np
##-- Model Function for creating the toy dataset
def func(param, X):
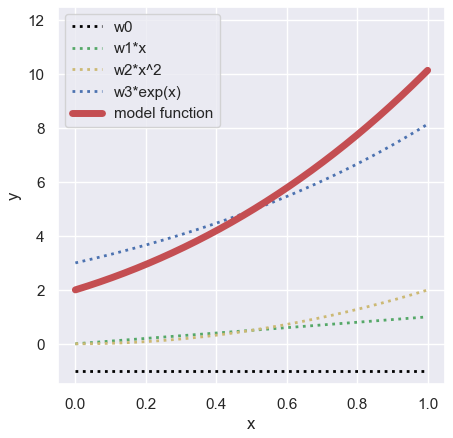
    return param[0] + param[1]*X + param[2]*np.power(X, 2) + param[3]*np.exp(X)

x = np.arange(0, 1, 0.01)
param = [-1.0, 1.0, 2.0, 3.0]

np.random.seed(seed=99) # Set Random Seed
y_model = func(param, x)
y_train = func(param, x) + np.random.normal(loc=0, scale=1.0, size=len(x))

Create a Toy Dataset by the Noise Function

Linear Regression Analyses

You can easily perform a linear regression analysis by the Scikit-learn module “LinearRegression()“. The procedure is as follows:

1. Create the instance of “LinearRegression()” as the name of “lr“
2. Train the model instance “lr” with the dataset by the “.fit()” module
3. Predict the training dataset by the “.predict()” module

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(x.reshape(-1, 1), y_train)
y_pred = lr.predict(x.reshape(-1, 1))

Possibly, you have the question that what does “x.reshape(-1, 1)” mean. The answer is that we have to prepare input variables “x” as a two-dimensional array. You will see the following error message if you prepare “x” as a one-dimensional array.

ValueError: Expected 2D array, got 1D array instead:
” *************** Here depends on your code *************** “
Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample.

In such a case, you have to convert “x” into a two-dimensional array by “x.reshape(-1, 1)“.

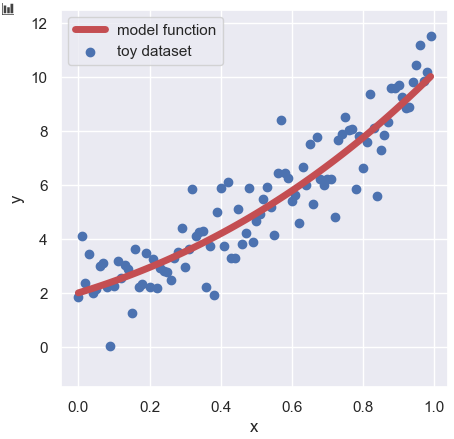
Congratulations!! Until here, the linear regression analysis is finished. You can confirm the result of your model as follows:

import matplotlib.pylab as plt
import seaborn as sns

plt.figure(figsize=(5, 5), dpi=100)
sns.set()
plt.xlabel("x")
plt.ylabel("y")
plt.ylim(-1.5, 12.5)
plt.scatter(x, y_train, lw=1, color="b", label="dataset")
plt.plot(x, y_pred, lw=5, color="r", label="linear regression")
plt.legend()
plt.show()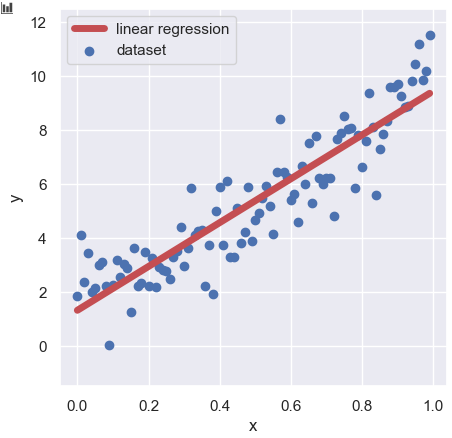

Summary

Contrary to the author’s intention, this blog has become a bit long. However, the important contents are as follows.

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(x.reshape(-1, 1), y_train)
y_pred = lr.predict(x.reshape(-1, 1))

The point is that you can perform a linear regression analysis with JUST the 4 line code! The roles of each line are below.

1. Import the module
2. Create the model
3. Train the model with the dataset
4. Predict

I would be glad if you think a linear regression is easy!

October 23, 2020December 24, 2020

Brief Explanation of the Theory of Linear Regression

Step-by-step to a Data Scientist > Blog > Machine Learning

A linear-regression technique is one of the basic analysis methods, so it may become the first attempt to investigate the relationship between independent variables and dataset.

In this post, we look through briefly the theory of linear regression. This article focuses on the concept of linear regression, so it will help the readers to understand with imagination.

Code implemented by Python

The implementation of the linear-regression model by Python is introduced by another post. This post is for just the brief theory with the simplified concept.

Python Shortcode for Linear Regression

What is the linear regression?

Linear regression is a technique to investigate the relationship between independent variables and a dataset. However, we assume that this relationship is linear. The most typical function would be:

$$y=ax+b,$$

Brief theory of linear regression

A representation of a linear regression is as follows:

$$y =\omega_{0}+\omega_{1}x_{1}+\omega_{2}x_{2}+…+\omega_{N}x_{N},$$

where $x_{i}$ is an independent variable and $\omega_{i}$ is a coefficient.

Besides, setting $x_{i}$ as $x_{1}=x$, $x_{2}=x^{2}$, and $x_{3}=e^{x}$, we can treat polynomial regression as the linear regression form:

$$y =\omega_{0}+\omega_{1}x+\omega_{2}x^{2}+\omega_{3}e^{x}.$$

The next step is to vectorize the above equation.

$$y=\left(\omega_{0}\ \omega_{1}\ \ldots\ \omega_{D}\right)\left(\begin{array}{ccc}1\\x_{1}\\\vdots\\x_{D}\\\end{array}\right).$$

$$\therefore y={\bf w^{T}}{\bf x},$$

where ${\bf w^{T}}$ is a coefficient vector and ${\bf x}$ is an independent variable vector. For the N dataset,

$$\left(\begin{array}{ccc}y_{1}\\y_{2}\\\vdots\\y_{N}\\\end{array}\right)=\left(\begin{array}{ccc}{\bf w^{T}}{\bf x_{1}}\\{\bf w^{T}}{\bf x_{2}}\\\vdots\\{\bf w^{T}}{\bf x_{N}}\\\end{array}\right).$$

As the matrix form, we can rewrite the above equation as follows:

$$\left(\begin{array}{ccc}y_{1}\\y_{2}\\\vdots\\y_{N}\\\end{array}\right)=\left(\begin{array}{ccccc}1&x_{11} &x_{12}&\ldots&x_{1D} \\1&x_{21} &x_{22}&\ldots&x_{2D}\\\vdots&&&&\vdots\\1&x_{N1} &x_{N2}&\ldots&x_{ND}\\\end{array}\right)\left(\begin{array}{ccc}\omega_{0}\\\omega_{1}\\\vdots\\\omega_{D}\\\end{array}\right).$$

$$\therefore{\bf y}\ ={\bf X}{\bf w}.$$

Our purpose is to estimate ${\bf w}$. Then, we will consider finding ${\bf w}$, which fits the dataset, namely minimizes the loss between the train data and the model-predicted data. We introduce the loss function of $E$ as follows:

$$\begin{eqnarray*}
E\left[ {\bf y}, {\bf \hat{y}}, {\bf X}; {\bf w} \right]\ &&=\sum^{n}_{n=1}\left(\hat{y}_{n} – y_{n} \right)^{2},\\ &&=\left({\bf \hat{y}} – {\bf X}{\bf w}\right)^{T}\left({\bf \hat{y}} – {\bf X}{\bf w}\right),
\end{eqnarray*}$$

where ${\bf \hat{y}}$ is the training data, and $E\left[ {\bf y}, {\bf \hat{y}}, {\bf X}; {\bf w} \right]$ is the loss between the train data(${\bf \hat{y}}$) and the model-predicted data(${\bf y}$). Note that this type of the loss function is called “Mean squared error”.

Here, we rewrite ${\bf w}$ as ${\bf w^{*}}$, which minimizes the loss $E\left[ {\bf y}, {\bf \hat{y}}, {\bf X}; {\bf w} \right]$, derived from the following relationship.

\begin{eqnarray*}
\dfrac{\partial E\left[ {\bf y}, {\bf \hat{y}}, {\bf X}; {\bf w} \right]}
{\partial {\bf w}} = 0
.
\end{eqnarray*}

From the above equation, we can obtain the solution ${\bf w^{*}}$ as follows:

\begin{eqnarray*}
\therefore
{\bf w^{*}}
=
\left(
{\bf X}^{T}{\bf X}
\right)^{-1}
{\bf X}^{T}
{\bf \hat{y}}
.
\end{eqnarray*}

Note that although the details of the derivation were skipped here, we can check the omitted process in the famous textbooks of machine learning or linear algebra.

The key is that all required information to estimate ${\bf w^{*}}$ is a training dataset(${\bf X}$ and ${\bf y}$). In addition, when we assume the form of the polynomial function, we can also judge the appropriateness of the assumed model.

Summary

We have briefly looked at the theory of linear regression. From the form of ${\bf w^{*}}=\left({\bf X}^{T}{\bf X}\right)^{-1}{\bf X}^{T}{\bf \hat{y}}$, you can understand that a linear regression analysis is on matric calculations.

In practice, there are few opportunities to be conscious of the calculation process. However, once you understand that linear regression is a matrix calculation, you can understand that the amount of calculation will become very large as the number of data increases.

October 23, 2020December 24, 2020

Create a Toy Dataset by the Noise Function

Step-by-step to a Data Scientist > Blog > Machine Learning

The toy dataset is useful when we attempt something new analysis method quickly, especially in regression analyses. In this post, we briefly see how to create a toy dataset with NumPy.

Then, let’s get started.

Import the Libraries

The code is written by Python. So firstly, we import the necessary library.

##-- For Numerical analyses
import numpy as np
##-- For Plot
import matplotlib.pylab as plt
import seaborn as sns

Define the Model Function

Here, we adopt the following function as an example.

$$y =-1+x+2x^{2}+3e^{x}.$$

The Python code for the above function is below.

def func(param, X):
    return param[0] + param[1]*X + param[2]*np.power(X, 2) + param[3]*np.exp(X)

For convenience, let’s create continuous data of x in the range 0 to 1 and check the behavior of the function.

x = np.arange(0, 1, 0.01)
param = [-1.0, 1.0, 2.0, 3.0]

y = func(param, x)

The behavior of (x, y) is as follows. The model function “y” is denoted by the red solid line. Note that, for visual clarity, the four polynomial terms, which construct the function, are added by the dashed line.

plt.figure(figsize=(5, 5), dpi=100)
sns.set()
plt.xlabel("x")
plt.ylabel("y")
plt.ylim(-1.5, 12.5)
plt.plot(x, y, lw=5, color="r", label="model function")
plt.legend()
plt.show()

Generate the Noise

Next, we prepare the toy dataset by adding the noise into the above function. The noise is generated by “the Gaussian distribution”, which is also called “the Normal distribution”. In this case, the noise function $\varepsilon(x)$ can be written as follows:

$$\begin{eqnarray*}
\varepsilon(x)=\frac{1}{\sqrt{2\pi\sigma^{2}}}
e^{-\dfrac{(x-\mu)^{2}}{2\sigma^{2}}},
\end{eqnarray*}$$

where $\mu$ is the mean and $\sigma$ the standard deviation.

We can easily use this noise function $\varepsilon(x)$ by the NumPy module “np.random.normal()“.

noise = np.random.normal(
                            loc   = 0,
                            scale = 1,
                            size  = 10000000,
                        )
plt.hist(noise, bins=100, color="r")

“loc“, “scale“, and “size“, the arguments of “np.random.normal()“, are the mean($\mu$), the standard deviation($\sigma$), and the size of the output. As seen in the graph below, we can confirm the Gaussian distribution.

The Model Function with Noise

The code for the function with the noise is as follows:

$$y =-1+x+2x^{2}+3e^{x} + \varepsilon(x).$$

##-- Set Random Seed
np.random.seed(seed=99)

y_toy = func(param, x) + np.random.normal(loc=0, scale=1.0, size=len(x))

Finally, you can get the toy dataset $(x, y_toy)$!!
You can confirm the behavior of the toy dataset as follows:

plt.figure(figsize=(5, 5), dpi=100)
sns.set()
plt.xlabel("x")
plt.ylabel("y")
plt.ylim(-1.5, 12.5)
plt.scatter(x, y_toy, lw=1, color="b", label="toy dataset")
plt.plot(x, y, lw=5, color="r", label="model function")
plt.legend()
plt.show()